Computational Neural Network Model of Cholinergic Activity in the Hippocampus

Abstract

An increasing body of research indicates that high cholinergic states in the hippocampus improve encoding ability while not affecting retrieval. While there exist previous computational models of cholinergic activity in the hippocampus (Hasselmo, 2006), they lack the descriptive power of more recent hippocampal models which incorporate theta rhythms and error-driven learning, increasing model capacity and yielding more robust results (Ketz, Morkonda, & O'Reilly, 2013). Here, I instantiate a neural network model of cholinergic effect in the hippocampus, capable of differentiating similar inputs under various levels of simulated cholinergic activity. The known effects of acetylcholine on subregional inhibition in the hippocampus along with simulated theta amplitude modification observed in biological studies were used to inform the computational model. Model testing revealed that high internal cholinergic states would significantly improve performance on input differentiation tasks while low cholinergic states would impair performance - results that are inline with previous literature. Individual testing of simulated cholinergic mechanisms revealed that dentate gyrus inhibition and theta rhythm amplitude effects are in support of existing literature and biological evidence. This work provides a foundation from which to address further questions about cholinergic effects on the hippocampus through a modernized simulation.

Introduction

The human hippocampus is critically involved in several functions including the formation and retrieval of memories and spatial navigation (Rudy, 2018). The investigation of these critical functions has led to the creation of a number of computational neural network models aimed at elucidating the underlying processes that allow the hippocampus (HPC) to work the way that it does. These networks have achieved impressive performance on tasks that cortical models have struggled with (Ketz, Morkonda, & O'Reilly, 2013). But hippocampi do not exist in a vacuum, they are constantly receiving neuromodulation from other brain regions. One such region is the basal forebrain (BF) and its release of acetylcholine (ACh) in the hippocampus is thought to affect learning and memory ability (Ballinger et al., 2016). As a result, there remains a lot of room for improving upon previous HPC neural network models by incorporating the dynamic effects of cholinergic modulation to answer important questions such as why we have the ability to remember past memories in vivid detail, but also sometimes fail to remember things that we know. Furthermore, having access to accurately represented cholinergic activity in the HPC could shed light on the underlying mechanisms of how age-related decline in cholinergic modulation relates to the observed parallel decline in memory performance (Richter et al., 2014).

The current research aims to instantiate a computational neural network model capable of executing pattern separation tasks under various levels of simulated cholinergic activity. Pattern separation (PS) is the act of breaking apart similar inputs into their own separate representations and is complemented by pattern completion (PC), which is the reactivation of a previously established representation from a partial cue (Sahay et al., 2011). At a network level, PS entails transforming similar inputs into dissimilar representations as the input moves along a network of regions, while PC requires the retrieval of full representations based on partial cues from preceding regions. The processes of pattern completion and pattern separation are themselves integral to human memory. For example, upon hearing the word ‘breakfast’, we can simultaneously understand that breakfast, in a general sense, is a meal eaten in the morning (pattern completion), but we can also differentiate between what we ate for breakfast this morning from yesterday (pattern separation). Given that the hippocampus is known to be crucial for both encoding and retrieval (Rudy, 2018) with existing pharmacological inactivation studies showing that deficits in the hippocampus leads to deficient pattern completion or pattern separation ability (Holt and Maren, 1999; Packard and McGaugh, 1996), the hippocampus must therefore be able to handle both PS and PC. But, as PS and PC seemingly oppose each other, there must be a way to activate or suppress one or the other - a task for which acetylcholine is thought to be a good candidate (Hasselmo, 2006). Below, I review the known effects of acetylcholine on the hippocampus, followed by the present state of computational modelling of the HPC.

Acetylcholine and the Hippocampus

Acetylcholine plays a vital role in the hippocampus’ ability to perform pattern separation tasks well. Rogers and Kesner (2004) found that scopolamine - a known ACh blocker - when injected directly into the CA3 region of a rat hippocampus performing a spatial memory task, impairs encoding (during which pattern separation is needed) but has no effect on retrieval (during which pattern completion is needed). Conversely, the researchers found that injections into the rat’s CA3 with physostigmine - a drug used to enhance the effects of ACh - had the opposite effect: no detriment to encoding but impaired retrieval. Atri et al. (2004) showed a similar result in humans. Participants injected with scopolamine showed impaired encoding, but similar retrieval as compared to the control. Though these studies were telling of the importance of acetylcholine in pattern completion and pattern separation tasks, an analysis of the particular mechanisms by which acetylcholine affects the hippocampus is critical for reproducing its effect in a computational model. The mechanisms through which acetylcholine interacts with the hippocampus are numerous and complex, but can be grouped into four overarching categories: inhibition, theta rhythms, long term potentiation, and disinhibition of pyramidal neurons. The first two are mechanisms that have been instantiated in the current computational model, while the second two are reviewed for the purpose of completeness.

Inhibition

The inhibition of neurons in particular hippocampal subregions by acetylcholine has been both researched in in vitro and in vivo model organisms, as well as being modelled computationally. The HPC is divided into a number of subregions which are thought to be particularly adept at specific tasks. Though there are others, this work will be mostly focused on the Entorhinal Cortex (EC), the Dentate Gyrus (DG), the CA3, and the CA1 regions of the hippocampus. Rodent research has demonstrated that acetylcholine inhibits dentate gyrus neurons, further promoting the sparsity already observed in this hippocampal region (Pabst et al., 2016). Furthermore, acetylcholine has been shown to inhibit recurrent collateral activity in the CA3 region along with biasing the CA1 region to novel input from the entorhinal cortex by suppressing excitatory CA3 to CA1 connections (Hasselmo & Schnell, 1994; Hasselmo, Schnell, & Barkai, 1995). These effects coupled together are thought to inhibit pattern completion ability but bolster pattern separation, with early hippocampal computational modelling successfully implicating high cholinergic levels with high degrees of inhibition in the mentioned regions, resulting in improved pattern separation (Hasselmo, Shnell, & Barkai, 1995). I selected this mechanism for implementation in the current work as previous modelling had already demonstrated its success, and the straight-forward nature of high ACh implying high inhibition in the DG and CA3 lends itself well to computational modelling and reproducibility.

Theta Rhythms

The coupling between cholinergic level and theta rhythms has been repeatedly observed in rodent models, with lesions to the septal hippocampal cholinergic system resulting in lower amplitude theta activity (Lee et al., 1994). Well established in vivo rodent studies have further demonstrated that higher acetylcholine levels in the hippocampus have been found to increase the amplitude of theta oscillations (Zhang et al., 2010). Theta rhythms, or theta oscillations, are a 4-12Hz wave found to be strongest in the hippocampal fissure, which either oscillates from 4-6Hz during immobility and REM sleep, or from 7-12Hz during voluntary movement and exploration (Kramis et al., 1975). Theta rhythms serve a number of functions within the hippocampus, acting as an internal clock, allowing for place cell encoding of spatial input, heightened plasticity, and enhanced memory ability (Lubenov & Siapas, 2009; Vertes, 2005). It is important to note, however, that though cholinergic neurons have been found to play a role in regulating theta rhythms (Apartis et al., 1998) the medial septum/diagonal band of Broca (MSDB), which projects both GABAergic and cholinergic neurons to the hippocampus, is responsible for theta rhythm generation (Xu et al., 2004).

Furthermore, optogenetic studies have confirmed that higher levels of acetylcholine in the hippocampus can increase HPC theta rhythm power while also showing that lower levels of acetylcholine cause sharp wave ripples (SWRs) to be more pronounced (Vandecasteele et al., 2014). And SWRs (150-200Hz) are commonly associated with supporting episodic memory consolidation (Buzsáki, 2015). The theta peak phase has been hypothesized to support memory encoding and pattern separation while the theta trough supports memory retrieval and pattern completion (Hasselmo, Bodelón, & Wyble, 2002).  Interestingly, rodent studies have also shown that during learning tasks, a synchronization effect can occur between theta waves and gamma waves (30-300Hz) in the hippocampus, which further supports synaptic change important for memory formation, storage and retrieval (Tort et al., 2009).

I selected the theta rhythm mechanism for implementation in the current computational neural network model for two reasons. First, as will be discussed in the next section, the framework from which the current model is built already has an implementation of theta rhythms in the hippocampus. Second, the theory of theta rhythms promoting encoding and pattern separation during the trough phase while promoting retrieval and pattern completion during the peak phase has been well supported by existing research (Hasselmo, 2006) and aligns well with research studying the inhibitory effects of acetylcholine mentioned earlier. Thus, it is the intention of this work to increase the accuracy of cholinergic modelling by also leveraging the theta oscillation mechanism.

Long Term Potentiation and Depression

The observed heightened synaptic plasticity from theta rhythms goes hand-in-hand with research demonstrating that acetylcholine can facilitate the long term potentiation (LTP) of synapses (Mitsushima, Sano, & Takahashi, 2013) - a mechanism thought to underlie learning and encoding (Martinez & Derrick, 1996). Thus, blocking cholinergic receptors impedes learning (Atri et al., 2004) while increasing activation of cholinergic receptors can increase learning capability (Levin, McClernon, & Rezvani, 2006). However, there is conflicting research in this area. Past rodent research has shown that weak muscarinic acetylcholine receptor (mAChR) activation results in LTP, while strong mAChR activation results in long term depression (LTD) (Auerbach & Segal, 1994). A potential explanation for this experimental contradiction is that some studies may not have taken into account research showing that synaptic input arriving during the positive phase of theta induces LTP while input arriving during the negative phase of theta induces LTD (Greenstein et al., 1988). Furthermore, much of the research investigating cholinergic-related LTP/LTD mechanisms has been done in vitro, which is prone to creating test environments which do not represent biological conditions, either through consistent and unfettered cholinergic activation, or through ACh doses significantly higher than would be experienced in an in vivo model. Despite these inconsistencies, there is other research showing that acetylcholine facilitates LTP between active CA3 and CA1 neurons (Blitzer et al., 1990).

Though the assumption that higher acetylcholine levels imply better pattern separation ability - as discussed in the sections above - will be maintained throughout this work, LTP-specific cholinergic modulation mechanisms will not be applied in the current model beyond the basic requirements of hebbian learning.

Disinhibition of Pyramidal Neurons

The final mechanism to be discussed is the disinhibition of pyramidal neurons due to acetylcholine. Above, I mentioned that while acetylcholine has dose-dependent effects, it also demonstrates partiality to particular kinds of neurons, with the ability to either inhibit or disinhibit their firing depending on the cell type. Goswamee and McQuiston (2019) conducted a rodent optogenetic study demonstrating that acetylcholine release increases the excitability of CA1 interneurons which in turn activate GABAB receptors on CA1 pyramidal cells, inhibiting Schaffer collateral fiber inputs in the stratum radiatum. Additionally, the excitability of CA1 interneurons was found to be governed by M3 muscarinic receptors specifically. However, if M2 muscarinic receptors on pyramidal cells were activated by acetylcholine, then perforant path fiber inputs in the stratum lacunosum-moleculare would be inhibited.  These results reaffirmed and built upon past work of pyramidal cell disinhibition in the CA1 such as Hasselmo and Schnell (1994). But, despite the interesting findings, this mechanism was not considered for implementation within the current model as the complexity of delineating individual neuronal groups with separate kinds of receptors was beyond the scope of this work.

Given the research reviewed above, both the inhibitory and theta rhythm mechanisms of cholinergic activity in the hippocampus were selected for pursuit in the current study, each to be implemented within the model in as physiologically-accurate a method as possible.

Computational Neural Network Modelling and the Hippocampus

Contemporary neural networks originated in the 1970s and were popularized in the 1980s under the name “Parallel Distributed Processing” (McClelland et al., 1986). These early implementations of Connectionist theory aimed to describe mental processes by using nets of connected nodes (or neurons) that pass input through hidden layer(s) of nodes to provide an output. The productive power of these artificial neural networks (ANNs) began being leveraged in the field of computer science for solving problems that functional machines struggled with, such as natural language processing, as well as in the field of neuroscience for modelling, using ANNs’ explanatory capability. Over time, computational neuronal networks have become increasingly valuable in neuroscience research as technological progress and theoretical breakthroughs have allowed for the creation of more complex and efficient models (Rubinov, 2015). These networks are able to shed light on underlying biological processes responsible for cognitive functions such as memory, learning, and more (Schapiro et al., 2017), and having access to robust and accurate computational models of brain regions can help explain behaviour and further the understanding of how the human brain works.

One of the first hippocampus-specific models (which also attempted to simulate cholinergic modulation in the HPC) that did not require any external tuning before training to achieve successful results was created by Michael Hasselmo (Hasselmo & Schnell, 1994), demonstrating that brain models did not require expressly set parameters unlike those previously created (Amit, 1992). This, and subsequent models, would leverage the increasingly well-known phenomenon of Hebbian learning as a foundation for how synaptic strength is regulated (Kelso, Ganong, & Brown, 1986; Hasselmo et al., 2020).

Following this, the Complementary Learning Systems theory (CLS) posited that the ability to remember unique events, but also have the ability to generalize across similar events are two processes fundamentally at odds with each other (McClelland, McNaughton, & O’Reilly, 1995). The CLS theory placed the hippocampus as the brain region responsible for rapidly picking apart recent experience into individual, separate memories. The cortex is then slowly taught these different memories and the memories remain stored in the cortex thereafter. The model proposed by McClelland, McNaughton, and O’Reilly (1995) consisted of a hippocampus and a layer for an associated cortex. But while the CLS theory accounted for learning occurring over time-spans of hours and days, the theory didn’t accommodate the idea that people can learn to group similar experiences very quickly (Schapiro et al., 2017).

The more recent Ketz, Morkonda, & O'Reilly, (2013) model sought to address the limits of Hebbian learning by introducing error-driven learning through the modelling of the theta-phase, allowing the hippocampus to switch rapidly between encoding and retrieval. This, along with additional factors such as bidirectional connectivity between the CA1 and EC allowed the model to surpass standard Hebbian learning capabilities in both storage capacity and performance (Ketz, Morkonda, & O'Reilly, 2013). The mechanism through which this was achieved was by the dynamic changing of strength of the hippocampal mono-synaptic (MSP) and tri-synaptic (TSP) pathways in time with the simulated theta rhythm. In the Ketz model, the MSP was composed of bidirectional EC to CA1 connections while the TSP consisted of unidirectional EC to DG to CA3 to CA1 paths. As a result, this model demonstrated rapid learning ability and addressed the CLS theory shortcoming of how people can quickly learn to generalize across experiences on short time-scales. Later work by Schapiro et al. (2017), using the Ketz model, established that the hippocampus could simultaneously handle the opposing processes of remembering individual episodes along with generalization in the case of a rapid learning scenario.

There also exist models of cholinergic function in the hippocampus, leveraging what is known of the biological function of acetylcholine in the HPC to further explain the HPC’s ability to both separate and generalize. One such model was built by Hasselmo (2006), but it included a smaller scale representation of the HPC and did not have a theta-rhythm component to rapidly interleave encoding and retrieval.

---

The purpose of this research is to instantiate a neural network model with error-driven learning and theta rhythm simulation along with a system of modulating cholinergic activity in the hippocampus in order to achieve a better understanding of how acetylcholine release from the basal forebrain affects human performance on pattern separation tasks. The neural network model used was based on the existing Ketz model of the HPC along with known physiological data that ACh inhibits recurrent connections but does not affect feedforward ones. Once the model was built and successfully trained on a created pattern separation dataset, the underlying structure and implementation of the model was modified to mirror high, low, and baseline cholinergic activity in the hippocampus. The following question was addressed: How does the hippocampus handle pattern separation tasks at various simulated cholinergic states?

Materials and Methods

Neural Network Model

In light of the current state of neural network modelling, Emergent v1.0.6 along with Leabra v1.0.4 were selected for their use of modern HPC models - specifically the Theta-phase HPC Ketz Model (Ketz, Morkonda, & O'Reilly, 2013) - along with their speed and ease of modification (Aisa, Mingus, & O’Reilly, 2008). The latest version of Emergent runs on Go, a statically typed and compiled programming language, generally used for its efficiency and speed. Emergent is complemented by Leabra, a package responsible for the underlying computational basis for biological neural networks. These two Go packages work in synchrony to provide a platform and graphical interface allowing the user to build, modify, train, and test neural networks.

This project used the existing pre-built Ketz HPC model that had already been implemented in Emergent as a baseline. The model architecture itself can be seen in Figure 1. Each square in each of the layers constitutes a unit, which can maintain a particular level of activity. This level of activity is always between 0 and 1 and the more yellow a unit is, the higher its activity at a given time.

The baseline model was modified in order to simulate low, medium, and high cholinergic states by modelling five key effects noted in the previous sections using the parameters available for configuration by Emergent and Leabra. First, dentate gyrus general layer inhibition was targeted with a high cholinergic state implying higher levels of general inhibition and a low cholinergic state implying lower levels, in line with findings from Pabst et al. (2016). Next, CA3 region general layer inhibition was increased to simulate a high cholinergic state and decreased to simulate a low cholinergic state. To model the inhibitory effects described in Hasselmo, Schnell, and Barkai (1995), CA3 recurrent collateral projections had their learning rate and relative input weight decreased at a high cholinergic level and increased at a low cholinergic level. The CA3 to CA1 Schaffer collaterals were manipulated by assigning a lower learn rate during a high cholinergic state to simulate biasing of the CA1 region to the entorhinal cortex while a low cholinergic state saw an increase in learning rate (Hasselmo & Schnell, 1994). Finally, the theta rhythm manipulation was modelled by altering how the Ketz model simulated the alternation between the trisynaptic pathway and monosynaptic pathway in the theta peak and theta trough, respectively. To simulate a higher amplitude in theta waves when a high level of acetylcholine was present (Zhang et al. 2010), the model was allowed to switch completely between the TSP and MSP stages where the CA1 region was driven by either CA3 recall or by the EC input layer with no interference from the other. In lower cholinergic states, however, the alternation between CA3 and EC input was only partial, resulting in the simulated theta wave being less effective, or suppressed.

The modification of these parameters for low, medium, and high cholinergic states were determined with the sigmoid function seen in Equation 1, where the input x represents the value assigned to a particular cholinergic state and f(x) is the cholinergic level, which provides the value multiplied against the baseline model parameter. This function was selected as it fulfills the following criteria: f(1)=1, leaving the model’s baseline value unchanged; there is a horizontal asymptote at f(x) = 2 demonstrating a point of saturation for cholinergic effect and the sigmoid nature of the function shows diminishing returns the more the level of acetylcholine is increased or decreased; f(0) = 0.238 indicating that even with no acetylcholine present (x=0), the model can still rely on alternative mechanisms to operate.

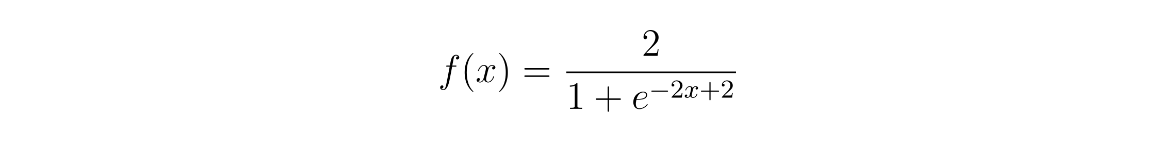
Four discrete models were used to simulate three cholinergic states - a low, a medium, and a high cholinergic state - which were compared to the unaltered model (baseline). The specific parameters used for these models can be found in Table 1. All other parameters not mentioned in Table 1 were kept identical to the baseline model. The full model weights for every tested scenario can be found in the supplementary material to this research.

Pattern Separation Task and Dataset

This model was trained on a dataset designed to test pattern separation ability. For each pair of stimuli, the model was trained to associate each input pattern with a different response. The correct response was provided during training but withheld during testing to determine how well the model had learned to discriminate between pair members. Figure 2 provides an example of one pair, including the training and testing set. Seven total pairs were created for this experiment with 0%, 20%, 40%, 60%, 80%, 90%, and 100% similarity between the pair members. The set with 100% similarity was used as a sanity check for which the model was expected to fail as the input patterns were identical between A1 and A2, but the expected output was completely different. The model was also expected to quickly learn the 0% similarity unit as no pattern separation would need to be done to discreetly characterize these units.

Training and Testing

The pattern separation task was performed as follows. The model was initialized in its baseline, low, medium, or high cholinergic state, as described above. The model was then stepped through a Run, containing up to 20 Epochs. Each Epoch consisted of a training event and a testing event for both the A1 input and A2 input. The training event would push the A1 training input set to the ‘Input’ layer, and allow the model to run for 100 cycles - arbitrary time units which allow the model to loop through the data a number of times. The same would then be done with the A2 unit, which would also run for 100 cycles. The testing event would then push the A1 testing input set to the ‘Input’ layer, and expect the correct output from ‘ECout’ after 100 cycles. The same would be done for A2. Once the Epoch was complete, the tests of A1 and A2 determine if the model has succeeded in learning both A1 and A2 by verifying that the activation pattern expected as output in ECout was reproduced to a satisfactory degree. If successful, the simulation would end, but if the model failed to learn either A1 or A2, or both, another Epoch would begin. Should another Epoch be needed, the model will continue this cycle of training and testing until the model either successfully learns the trial or unsuccessfully completes 20 Epochs, which constitutes a failure.

The number of Epochs needed to learn the trial along with the unit activation values were logged for each run for analysis. Each of the low, medium, high, and baseline models were given 50 runs for each similarity condition, with an average number of Epochs needed being calculated and used as the metric of task performance.

Pattern Separation Analysis

In order to verify that the model was performing pattern separation during the task, as intended, additional analysis was conducted on the unit activation patterns in the hidden layers of the network. For each run and every similarity condition, the following analysis was conducted. The settled activity (after 99 of 100 cycles) of the first Epoch of every run was taken and the spearman correlation between the A1 and A2 trials was calculated for the unit activation pattern for every layer. From here, the correlation value of the given layer was subtracted from the layer preceding it following the rough hippocampal circuit of: ECin, DG, CA3, CA1, ECout. This means that the correlation value for a given run for the dentate gyrus layer was subtracted from the correlation value of the EC in layer for the same run. The aim was to observe what effect different levels of acetylcholine had on the ability of the hidden layers to decorrelate or correlate a given activation pattern.

Results

A set of experiments were performed where the model was run for every condition for all tasks 50 times. The first experiment saw the inclusion of all cholinergic modifications described above with results shown in Figure 3. In Figure 3B, we can see that model performance is very similar up until 80% input similarity. At 90%, however, there is a distinction in performance with the high cholinergic state performing the best, the low cholinergic state performing the worst. Note that the lower the y-value at a given level of similarity, the better the model performance. Figure 3A shows a more in-depth look at how cholinergic state affects each hidden layer with the DG and CA1 layers being the most differentially affected by cholinergic state when all modifiers are active. Furthermore, the CA3 region demonstrates mostly positive correlation values across all similarity conditions, but the dentate gyrus and CA1 region flip from negative to positive correlation values and vice versa depending on the cholinergic condition.

Figures 4 to 8 focus on model performance when all parameters are kept at baseline apart from one target parameter. The purpose of these experiments was to identify the effect of isolated cholinergic mechanisms on model performance and gain insight into how they contribute to model performance overall. Generally, we observe the trend of a high cholinergic state performing better on the pattern separation task than the low cholinergic state at high levels of input similarity with all models performing comparably at 60% input similarity or lower. All of the modifiers used in Figures 4 through 8 were also used in the final combined model with the results displayed in Figure 3.

In Figure 4, only the dentate gyrus general layer inhibition parameter was manipulated. A modifier of 0.6 was used for the low cholinergic state, 0.7 for medium, 0.8 for high, and 1.0 for baseline. This modifier acted as the input into Equation 1, the output of which was multiplied by the baseline model parameter to yield the final parameter. Equation 1 was used as a processing step for the parameters of all mechanisms implemented in this model with the exception of the theta rhythm mechanism. In Figure 4A, we see that the DG layer maintains a correlation value under 0 regardless of the cholinergic state while the CA3 and CA1 regions remain mostly above 0. In Figure 4B, the baseline model took the longest to learn that task on the higher similarity trials while the high cholinergic state learned the fastest.

In Figure 5, only the CA3 general layer inhibition parameter was manipulated. The low cholinergic state used a modifier of 0.8, the medium state used 0.9, and the high state used 1.3. In Figure 5A, The DG maintains a correlation value under 0 regardless of the cholinergic state while the CA3 region begins with a positive correlation which becomes negative as trial similarity increases. CA1 layer correlation remained positive throughout all conditions. Figure 5B shows that as the cholinergic modifier increased, the performance of the model on the pattern separation task improved.

Figure 6 shows the effect of manipulating only parameters relevant to the CA3 recurrent collaterals: the learning rate and relative input weight scaling. The low cholinergic state used a modifier of 1.5, the medium state used 1 (the same as baseline), and the high state used 0.3. Figure 6A shows that the DG maintains a correlation value under 0 regardless of the cholinergic state while the CA3 region begins with a positive correlation which becomes negative as trial similarity increases. CA1 layer correlation remained positive throughout all conditions. In Figure 6B, we see that the low cholinergic condition performs worse than all the other conditions at 90% similarity.

In Figure 7, only the CA3 to CA1 Schaffer collaterals were modified based on cholinergic level. The low cholinergic state used a modifier of 1.3, the medium state used 1.2, and the high state used 0.5. Figure 7A shows that the DG maintains a correlation value under 0 regardless of the cholinergic state while the CA3 region begins with a positive correlation which becomes negative as trial similarity increases. CA1 layer correlation remained positive throughout all conditions. In Figure 7B, we see that the low cholinergic state performed worse than the medium, high, and baseline states at 90% input similarity. Otherwise all models performed similarly for all other conditions.

In Figure 8, only the theta rhythm manipulations were included.  The low cholinergic state used a theta modifier of 0.4, the medium state used 0.3, and the high state used 0 (same as baseline). Unlike the other modifiers, the theta modifier was not inputted into Equation 1, and instead directly affected how the network learned in theta peaks and theta troughs. In Figure 8A, we see that the DG maintains a correlation value under 0 regardless of the cholinergic state for all states with the exception of the low cholinergic state, which saw a correlation slightly over 0 for some similarity conditions. The CA3 region generally remained above 0, but as the trial similarity increased, the correlation fell below 0. The CA1 layer correlation remained positive throughout all conditions. In Figure 8B, we once again observe that lower levels of simulated acetylcholine resulted in better task performance overall.

Figures 6A and 7A show a particularly small difference between correlation values depending on cholinergic state with the changes in these cases affecting the projections between regions and not the regions themselves. Despite this, there are still noticeable differences in model performance with a given cholinergic state in Figure 6B and Figure 7B. Figures 4A, 5A, and 8A show the greatest differences in correlation of the low, medium, and high cholinergic states and the baseline state.

Finally, Figure 9 demonstrates model behaviour when all of the selected inhibitory mechanisms of acetylcholine have been implemented, but the theta amplitude remains at baseline for all conditions. The parameters used to model each of the findings listed were the same as the ones described in the individual experiments in Figures 4-7. The theta modifier was set to 0 (same as baseline) for all conditions. In Figure 9A, we see the DG correlation values remain under 0 for all conditions. The CA3 region correlation values remain over 0 for all conditions with the exception of the baseline condition which crosses over into negative correlation values as trial similarity increases. The CA1 region retains a positive correlation for all conditions. We also note that the CA3 region and CA1 region correlations for the low, medium, and high conditions stray from the baseline condition by a large margin, but the DG correlations stay roughly on par with the baseline. Figure 9B shows that the baseline model performs significantly worse than all the other conditions in the 90% similarity trial while the high and medium cholinergic state perform roughly the same. The low cholinergic state, however, performs significantly better than all other models in the 90% similarity case.

Discussion

This work provides a promising first step for updating previous well known cholinergic models of the hippocampus, namely Hasselmo (2006), which focused on altering levels of inhibition in specifically the CA3 recurrent connections and in the CA3 layer. Building on previous work, my model instantiation makes use of error-driven learning and theta-rhythm simulation to create a more modern and robust working cholinergic model.

With five different modifications made to the model to simulate particular cholinergic states, we can look at both the modifications’ individual effects on task performance and correlation effects as well as cumulatively based on the results in Figures 3 through 9.

All Modifications

Figure 3 displays the combined effects of all cholinergic modifications and, at the 90% similarity case in Figure 3B, shows that the low cholinergic state performs similarly to the baseline model, taking an average of 14-15 Epochs to learn the task where the medium cholinergic state takes around 12-13 and the high cholinergic state takes about 10. So, by simulating the biological effects of acetylcholine discussed previously: increased dentate gyrus inhibition, increased CA3 inhibition, reduced CA3 recurrent collateral learning, reduced Schaffer collateral learning, and decreased theta amplitude, we can confirm that a high cholinergic state significantly improves pattern separation task performance as compared to a low cholinergic state. However, when we look at Figure 3A and analyze how the input patterns are decorrelated or correlated across layers, we see that the picture is not necessarily so clear. First, it is important to note that all correlations for every hidden layer will tend to 0 at 100% input similarity as the A1 and A2 trials are identical for that trial, resulting in identical activation patterns, and thus perfect spearman correlation values of 1. Thus, if you subtract a given layer’s 100% similarity correlation of 1 from the preceding layer’s correlation value of 1, you will always end up with a net 0 difference in correlation. What matters here is how correlation changes up until the 100% input similarity condition. Since pattern separation is, by definition, a decorrelation of similar inputs, we can say that pattern separation is occurring in a given layer for a given condition if the correlation value is less than 0, as this will imply that the current layer had a lesser correlation than the layer preceding it, and was thus decorrelating. Conversely, if the correlation value is above 0, pattern completion is implied. In Figure 3A, we see that while the baseline dentate gyrus pattern separates for all similarity conditions - in line with its expected function given its known sparsity and role in pattern separation, both the low and medium cholinergic conditions actually pattern complete for similarity conditions of 40% and up. On the other hand, the CA1 region, known for its role in pattern completion, actually starts conducting pattern separation in the low and medium cholinergic conditions after 50% input similarity. This finding seems to contradict intuition as one would assume that the more challenging a pattern separation task became, the more the dentate gyrus would need to pattern separate, complemented by more extensive pattern completion by the CA1.

One possible explanation here is that, in the low cholinergic state, the dentate gyrus general layer inhibition parameter actually drops slightly lower than the CA1 layer general inhibition with 2.28 and 2.4 respectively, causing the CA1 region to be more effective at pattern separation than the dentate gyrus due to its higher sparsity, resulting in the observed role swap. This is not the case in the high cholinergic level where the dentate gyrus general inhibition is at 3.05 whereas the CA1 general inhibition remains at 2.4. One question that remains to be answered following this logic, is why the DG and CA1 swap roles in the medium cholinergic condition where dentate gyrus inhibition is 2.69 while CA1 inhibition is still 2.4. On its own, this question is difficult to answer as we are observing all of the modelled cholinergic effects affecting each other, but a more granular investigation of each effect provides a clearer picture.

Dentate Gyrus Inhibition

Figure 4 targets dentate gyrus inhibition and here we begin to see more explicit support for Pabst et al. (2016) when looking at the dentate gyrus graph in Figure 4A. We see that for most similarity conditions, higher DG inhibition directly implies higher levels of pattern separation. The baseline model offers the highest level of inhibition: 3.8, followed by the values mentioned in Table 1 for high, medium, and low cholinergic states. We also see complementary results in the CA1 region, with higher levels of DG inhibition requiring higher levels of CA1 pattern completion. The effect that DG general inhibition modulation has on pattern separation task performance is not as straightforward, however. We appear to get conflicting results with the baseline performing the poorest followed by the medium, then low cholinergic state - with the high cholinergic state performing the best. The results in Figure 4B seem to imply that model task performance, while instructive, is not solely indicative of expected pattern separation performance.

One possible explanation for this observation is that despite the task being designed around the idea of needing to separate out two increasingly similar inputs, pattern completion must still play a role in model performance, as the model is expected to reproduce the proper strong left or strong right pattern depending on which pattern it receives as input. Thus, a solution targeting exclusively pattern separation ability will not necessarily produce the most performant model. However, model performance coupled with the correlation graphs can help explain more clearly exactly what the effects of certain parameter manipulations imply.

CA3 Inhibition

The effects of CA3 region general inhibition in Figure 5 are more intuitively defined with higher layer inhibition implying better task performance. The worst performer was the low cholinergic state with a 0.8 modifier, followed by medium with 0.9, baseline with 1, and high with 1.3 being the best performer. The interesting insight here is that Figure 5A did not reveal any major differences across conditions with all layers grouping close to the baseline despite the very clear differences in pattern separation task performance. Though this particular mechanism of cholinergic effect is not drawn directly from any biological research, the consistent effect may be indicative of the fact that increased acetylcholine does increase general region inhibition alongside the known effects of increasing CA3 recurrent collateral inhibition (Hasselmo et al., 1995). Despite the inconclusive nature of Figure 5A, further testing in the form of a correlational analysis in the last training Epoch, after all the learning has occurred, as opposed to the first Epoch as performed here, might reveal some differences, particularly in the CA3 region correlations as CA3 recall to the CA1 region is an important part of the pattern completion procedure when the model produces its output.

CA3 Recurrent Collaterals

The inclusion of the CA3 recurrent collateral suppression method was inspired by Hasselmo et al. (1995) with their findings showing that low levels of acetylcholine in the CA3 recurrent collaterals pushed the layer to recall existing stored patterns, while high levels pushed the layer to learn new patterns without the help of previously stored patterns. Despite this existing evidence, the suppression of the learning rate and input weight scaling of the CA3 recurrent collateral projections - mimicking inhibition - did not seem to lead to much better pattern separation task performance with Figure 6B showing the low cholinergic state performing the worst but all other states performing similarly to each other. Furthermore, there were no major differences between correlations in Figure 6A as all correlations remained near the baseline across similarity conditions. These findings do not necessarily go against the Hasselmo et al. (1995) claim that increasing inhibition in the CA3 recurrent collaterals bolsters pattern separation, as the current model does not directly increase inhibition in these projections since a parameter like this does not exist for projection types. Further experiments should aim to differently modify the learning rate of the projections and the input weight scaling to more closely mimic increases in inhibition. Concretely, additional acetylcholine may instead increase the rate of learning but decrease the weight scaling as a means to illustrate learning without using recall, as suggested in the Hasselmo et al. (1995) study.

CA3 to CA1 Schaffer Collaterals

The Schaffer collateral modifications did yield slightly more differentiated results for model performance for the 90% similarity trial than the CA3 recurrent collaterals did. In Figure 7B, the low cholinergic state performing the worst followed by medium, high, and baseline all performing slightly better, but the results are still quite similar to the CA3 recurrent collateral results in Figure 6. Concretely, there were no major and consistent differences in correlations in Figure 7A with all conditions roughly following the baseline in all tests. This mechanism was intended to replicate Hasselmo and Schnell (1994) and their theory that increased acetylcholine biases the CA1 to ECin rather than to CA3. Thus, the learning rate of these projections was reduced in the high cholinergic state while being increased in the low cholinergic state, aiming to replicate the bias. Future experiments targeting these projections should aim to modify alternative parameters related to the suppression of the Schaffer collaterals or, alternatively, improve the strength of ECin to CA1 projections to further strengthen the bias.

Theta Amplitude

The effect of the theta manipulation mechanism did yield significant and interesting results to both correlation values and task performance in Figure 8. First, in Figure 8B, the low cholinergic state with the lowest theta amplitude performed significantly worse than the medium and high states (the high state was equivalent to the baseline). Next, in Figure 8A, higher theta amplitudes seemed to improve the extent of pattern separation in the dentate gyrus and improved the extent of pattern completion in the CA1 in a complimentary fashion. The CA3 region saw a slight increase in pattern separation given an increased theta amplitude. It is not straightforward, however, to state that this result appears to support the findings of Zhang et al. (2010) or Vandecasteele et al. (2014) as the increase of the theta rhythm amplitude was directly and purposefully tied to an increase in acetylcholine in the model with no causality involved. However, the idea that enhanced theta power improves pattern separation performance in the hippocampus does provide additional insight into why theta rhythms may be crucial for governing pattern completion and pattern separation in the HPC and lends further support to the underlying key ideas behind the Complementary Learning Systems model (McClelland, McNaughton, & O’Reilly, 1995).

Inhibitory Effects Only

Finally, the most surprising - and seemingly contradictory - result was shown in Figure 9B, where the low cholinergic state model outperformed the baseline, medium, and high cholinergic state models on all high similarity conditions despite the fact that on each individual tested inhibitory result (Figures 4-7), the low cholinergic state performed worse than the others. But given the correlation results in Figure 9A, the model performance may have more to do with limitations of the task provided and how the hidden layers were able to adapt to the new parameters than portray evidence against the various cholinergic mechanisms discussed above. Concretely, all the effects together not only decreased the degree of pattern separation in the DG as compared to the baseline, but also decreased the degree of pattern completion in the CA1. Furthermore, the baseline model saw the CA3 region tend towards pattern separation for high similarity trials whereas the combined inhibitory models did the opposite and remained firmly on the pattern completion side. Interestingly, all three of the tested models performed significantly better overall on the tasks than the baseline did, but this calls into question if the parameters selected for the different cholinergic states normalized the parameters of each hidden layer too much, which caused the DG, CA3, and CA1 to act as three generic hidden layers and perform well on the task simply because of that. In a biologically based hippocampus, these layers might have more distinct features which may sacrifice task performance for biological relevance. This can be validated in future experiments by maintaining layer size, but configuring all hidden layers with the same parameters and testing how this model handles the task.

Conclusions and Future Directions

Though there continue to be a number of worthwhile experiments left to perform on this model to get to the bottom of why certain mechanisms perform the way they do, the results presented above are supportive of two key findings. First, acetylcholine increases inhibition in the dentate gyrus and results in stronger pattern separation. Second, theta rhythm amplitude is critical to model pattern separation ability with higher levels of acetylcholine and higher theta amplitudes implying increased pattern separation. However, there are a number of additional extensions besides the ones discussed above that would improve the utility of the models I have created when targeting the eventual goal of learning more about human hippocampal behaviour and the specific role that acetylcholine plays therein.

First and foremost, the model will be validated against human behavioural pattern separation results with the goal of providing granular insight into cholinergic activity within the human hippocampus based on a particular participant’s PS task results. If the model can be tuned to perform similarly to a healthy control group of participants, it could be possible to identify people who may have cholinergic deficits from behaviour alone. Similarly, using participant fMRI data to inform the model of expected pattern separation task performance based on observed basal forebrain integrity would extend the use-cases of this model even further.

Another extension of the current research would be to simulate cholinergic activity in a continuous manner, as opposed to relying on discrete states to produce results. This could involve the modelling and implementation of a basal forebrain region with manipulatable integrity parameters used to simulate the extent to which an individual would be able to fluctuate cholinergic levels in their hippocampus. Using participant fMRI data to further refine the model has the potential to provide even more precise information on potential cholinergic deficits of participants who perform abnormally on pattern separation tasks.

Though the question of why we have the ability to remember past memories in vivid detail, but also sometimes fail to remember things that we know, goes unanswered, the model instantiated here has taken a step towards showing that complex observable biological phenomena in living brains can be modelled and reinforced in a computational setting that can hopefully begin to reveal the specifics of how complex neuromodulatory interactions govern neural behaviour on a scale more specific than possible in in-vivo models. But, despite the fact that this research leaves many questions open to future work, the current state of the project is encouraging - with data corroborating previous models along with biological evidence and creating a strong foundation from which to address deeper and more intricate questions later on.

References

Aisa, B., Mingus, B., & O’Reilly, R. (2008). The Emergent neural modeling system. Neural Networks, 21(8), 1146–1152. https://doi.org/10.1016/j.neunet.2008.06.016

Amit, D. J. (1992). Modeling brain function: The world of attractor neural networks. Cambridge university press.

Apartis, E., Poindessous-Jazat, F. R., Lamour, Y. A., & Bassant, M. H. (1998). Loss of rhythmically bursting neurons in rat medial septum following selective lesion of septohippocampal cholinergic system. Journal of Neurophysiology, 79(4), 1633–1642.

Atri, A., Sherman, S., Norman, K. A., Kirchhoff, B. A., Nicolas, M. M., Greicius, M. D., … Stern, C. E. (2004). Blockade of central cholinergic receptors impairs new learning and increases  proactive interference in a word paired-associate memory task. Behavioral Neuroscience, 118(1), 223–236. https://doi.org/10.1037/0735-7044.118.1.223

Auerbach, J. M., & Segal, M. (1994). A novel cholinergic induction of long-term potentiation in rat hippocampus. Journal of Neurophysiology, 72(4), 2034–2040.

Ballinger, E. C., Ananth, M., Talmage, D. A., & Role, L. W. (2016). Basal Forebrain Cholinergic Circuits and Signaling in Cognition and Cognitive Decline. Neuron, 91(6), 1199–1218. https://doi.org/10.1016/j.neuron.2016.09.006

Blitzer, R. D., Gil, O., & Landau, E. M. (1990). Cholinergic stimulation enhances long-term potentiation in the CA1 region of rat hippocampus. Neuroscience Letters, 119(2), 207–210.

Buzsáki, G. (2015). Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning. Hippocampus, 25(10), 1073–1188. https://doi.org/10.1002/hipo.22488

Goswamee, P., & McQuiston, A. R. (2019). Acetylcholine release inhibits distinct excitatory inputs onto hippocampal CA1 pyramidal neurons via different cellular and network mechanisms. Frontiers in Cellular Neuroscience, 13, 267.

Greenstein, Y. J., Pavlides, C., & Winson, J. (1988). Long-term potentiation in the dentate gyrus is preferentially induced at theta rhythm periodicity. Brain Research, 438(1–2), 331–334.

Hasselmo, M. E., Schnell, E., & Barkai, E. (1995). Dynamics of learning and recall at excitatory recurrent synapses and cholinergic modulation in rat hippocampal region CA3. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience, 15(7 Pt 2), 5249–5262. https://doi.org/10.1523/JNEUROSCI.15-07-05249.1995

Hasselmo, M. E. (2006). The role of acetylcholine in learning and memory. Current Opinion in Neurobiology, 16(6), 710–715. https://doi.org/10.1016/j.conb.2006.09.002

Hasselmo, M. E., Bodelón, C., & Wyble, B. P. (2002). A proposed function for hippocampal theta rhythm: separate phases of encoding and retrieval enhance reversal of prior learning. Neural Computation, 14(4), 793–817. https://doi.org/10.1162/089976602317318965

Hasselmo, M. E., & Schnell, E. (1994). Laminar selectivity of the cholinergic suppression of synaptic transmission in rat hippocampal region CA1: computational modeling and brain slice physiology. Journal of Neuroscience, 14(6), 3898–3914.

Hasselmo, M. E., Alexander, A. S., Dannenberg, H., & Newman, E. L. (2020). Overview of computational models of hippocampus and related structures: Introduction to the special issue. Hippocampus, 30(4), 295–301. https://doi.org/10.1002/hipo.23201

Holt, W., & Maren, S. (1999). Muscimol inactivation of the dorsal hippocampus impairs contextual retrieval of fear memory. Journal of Neuroscience, 19(20), 9054–9062.

Kelso, S. R., Ganong, A. H., & Brown, T. H. (1986). Hebbian synapses in hippocampus. Proceedings of the National Academy of Sciences, 83(14), 5326–5330.

Ketz, N., Morkonda, S. G., & O’Reilly, R. C. (2013). Theta Coordinated Error-Driven Learning in the Hippocampus. PLoS Computational Biology, 9(6). https://doi.org/10.1371/journal.pcbi.1003067

Kramis, R., Vanderwolf, C. H., & Bland, B. H. (1975). Two types of hippocampal rhythmical slow activity in both the rabbit and the rat: relations to behavior and effects of atropine, diethyl ether, urethane, and pentobarbital. Experimental Neurology, 49(1), 58–85.

Lee, M. G., Chrobak, J. J., Sik, A., Wiley, R. G., & Buzsaki, G. (1994). Hippocampal theta activity following selective lesion of the septal cholinergic system. Neuroscience, 62(4), 1033–1047.

Levin, E. D., McClernon, F. J., & Rezvani, A. H. (2006). Nicotinic effects on cognitive function: behavioral characterization,  pharmacological specification, and anatomic localization. Psychopharmacology, 184(3–4), 523–539. https://doi.org/10.1007/s00213-005-0164-7

Lubenov, E. V, & Siapas, A. G. (2009). Hippocampal theta oscillations are travelling waves. Nature, 459(7246), 534–539. https://doi.org/10.1038/nature08010

Martinez, J. L., & Derrick, B. E. (1996). Long-Term Potentiation and Learning. Annual Review of Psychology, 47(1), 173–203. https://doi.org/10.1146/annurev.psych.47.1.173

McClelland, J. L., McNaughton, B. L., & O’Reilly, R. C. (1995). Why there are complementary learning systems in the hippocampus and neocortex:  insights from the successes and failures of connectionist models of learning and memory. Psychological Review, 102(3), 419–457. https://doi.org/10.1037/0033-295X.102.3.419

McClelland, J. L., Rumelhart, D. E., Group, P. D. P. R., & others. (1986). Parallel distributed processing. Explorations in the Microstructure of Cognition, 2, 216–271.

Mitsushima, D., Sano, A., & Takahashi, T. (2013). A cholinergic trigger drives learning-induced plasticity at hippocampal synapses. Nature Communications, 4. https://doi.org/10.1038/ncomms3760

Pabst, M., Braganza, O., Dannenberg, H., Hu, W., Pothmann, L., Rosen, J., … Beck, H. (2016). Astrocyte Intermediaries of Septal Cholinergic Modulation in the Hippocampus. Neuron, 90(4), 853–865. https://doi.org/10.1016/j.neuron.2016.04.003

Packard, M. G., & McGaugh, J. L. (1996). Inactivation of hippocampus or caudate nucleus with lidocaine differentially affects expression of place and response learning. Neurobiology of Learning and Memory, 65(1), 65–72.

Richter, N., Allendorf, I., Onur, O. A., Kracht, L., Dietlein, M., Tittgemeyer, M., … Kukolja, J. (2014). The integrity of the cholinergic system determines memory performance in healthy elderly. NeuroImage, 100, 481–488. https://doi.org/10.1016/j.neuroimage.2014.06.031

Rogers, J. L., & Kesner, R. P. (2004). Cholinergic Modulation of the Hippocampus during Encoding and Retrieval of Tone/Shock-Induced Fear Conditioning. Learning and Memory, 11(1), 102–107. https://doi.org/10.1101/lm.64604

Rubinov, M. (2015). Neural networks in the future of neuroscience research. Nature Reviews Neuroscience, 16(12), 767. https://doi.org/10.1038/nrn4042

Rudy, J. W. (2018). The Neurobiology of Learning and Memory (Second Edi). Sinauer Associate, Inc. Publishers.

Sahay, A., Wilson, D. A., & Hen, R. (2011). Pattern separation: a common function for new neurons in hippocampus and olfactory bulb. Neuron, 70(4), 582–588. https://doi.org/10.1016/j.neuron.2011.05.012

Schapiro, A. C., Turk-Browne, N. B., Botvinick, M. M., & Norman, K. A. (2017). Complementary learning systems within the hippocampus: A neural network modelling approach to reconciling episodic memory with statistical learning. Philosophical Transactions of the Royal Society B: Biological Sciences, 372(1711). https://doi.org/10.1098/rstb.2016.0049

Tort, A. B. L., Komorowski, R. W., Manns, J. R., Kopell, N. J., & Eichenbaum, H. (2009). Theta–gamma coupling increases during the learning of item–context associations. Proceedings of the National Academy of Sciences, 106(49), 20942–20947.

Vandecasteele, M., Varga, V., Berényi, A., Papp, E., Barthó, P., Venance, L., … Buzsáki, G. (2014). Optogenetic activation of septal cholinergic neurons suppresses sharp wave ripples  and enhances theta oscillations in the hippocampus. Proceedings of the National Academy of Sciences of the United States of America, 111(37), 13535–13540. https://doi.org/10.1073/pnas.1411233111

Vertes, R. P. (2005). Hippocampal theta rhythm: A tag for short‐term memory. Hippocampus, 15(7), 923–935.

Xu, C., Datta, S., Wu, M., & Alreja, M. (2004). Hippocampal theta rhythm is reduced by suppression of the H‐current in septohippocampal GABAergic neurons. European Journal of Neuroscience, 19(8), 2299–2309.

Zhang, H., Lin, S.-C., & Nicolelis, M. A. L. (2010). Spatiotemporal coupling between hippocampal acetylcholine release and theta oscillations in vivo. Journal of Neuroscience, 30(40), 13431–13440.